The Pythagorean Theorem Activity
The
Pythagorean Theorem states that in a right triangle with legs of lengths a
and b and hypotenuse of length c, ![]() (See Figure1a.)
The theorem appears as Proposition 47 of Book I of Euclid's Elements. Euclid attributes it to
Pythagoras(approximately 580-500 BCE), but it almost certainly was known much
earlier to Egyptian, Mesopotamian, Chinese, and Indian mathematicians.
(See Figure1a.)
The theorem appears as Proposition 47 of Book I of Euclid's Elements. Euclid attributes it to
Pythagoras(approximately 580-500 BCE), but it almost certainly was known much
earlier to Egyptian, Mesopotamian, Chinese, and Indian mathematicians.
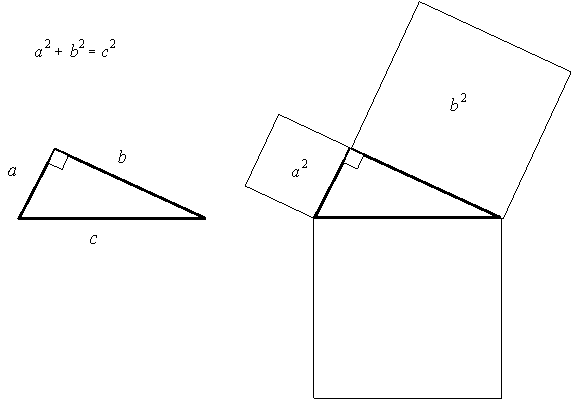
Figure 1a Figure 1b
You undoubtedly have used the Pythagorean Theorem as a tool for finding the length of the third side of a right triangle when the lengths of two sides are given. Notice, however, that the Pythagorean Theorem is a statement about squares, namely a2, b2, and c2. It shouldn't surprise you, then, that Euclid and his predecessors thought of the Pythagorean Theorem as a statement about areas of squares and visualized it as in Figure 1b.
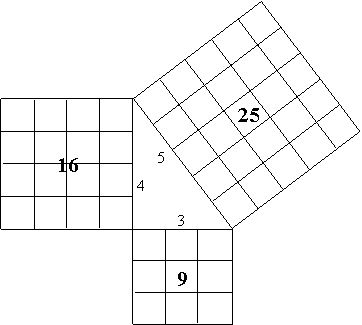 |
Figure 2
The diagram in Figure 2 of the special case of the 3-4-5 right triangle appeared in the Chinese text, Nine Chapters on the Mathematical Art, which was originally composed in about200 BCE and rewritten and expanded in about 250 CE by Liu Hui. Like Euclid's Elements, the Nine Chapters was a compilation of the mathematics known to that day (Swetz and Kao, 17, 26-27). In fact, the Pythagorean Theorem appears in an older Chinese text, The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven, probably written during the sixth century BCE, the time of Pythagoras, and consisting of results known up to that time (Swetz and Kao, 14).
Many ancient proofs of the Pythagorean Theorem employ geometric algebra; that is, they rely on finding the area of a given figure in two different ways. Figure 3illustrates one such proof. Viewing the figure as a square with side length c, the area of the figure is c2. On the other hand, dissecting the figure into four right triangles and one small square, as shown, yields area
![]()
Equating these two formulas for the area of the large square, we obtain
![]()
or ![]()
or ![]()
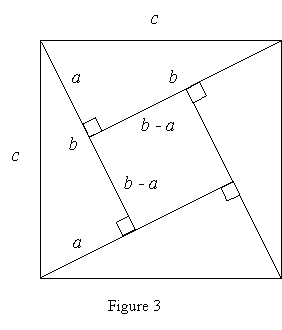
This proof often is credited to the Indian mathematician Bhaskara (1114-1185 CE), but it appeared much earlier in the Chinese text, The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven (Swetz and Kao, 13-15).
1. Use the Pythagorean Theorem to find the length of the third side of the right triangle.
 |
 1a.
1b.
1a.
1b.

1c.
2. The converse of the Pythagorean Theorem says: If a triangle has sides of lengths a, b, and c and a2 + b2 = c2, then the triangle is a right triangle with legs of lengths a and b and hypotenuse of length c. Use the Pythagorean Theorem and its converse to determine whether or not each triangle is a right triangle.
 |
|||
 |
|||
2a. 2b.

2c.
3. Here
is another proof of the Pythagorean Theorem that uses geometric algebra. Complete
the proof by writing the area of the large square shown in Figure 4 in two
different ways. Then equate your two formulas for the area of the square and
simplify to obtain ![]() A version of this proof
appears in the Chinese text, Arithmetical Classic of the Gnomon and the
Circular Paths of Heaven.
A version of this proof
appears in the Chinese text, Arithmetical Classic of the Gnomon and the
Circular Paths of Heaven.
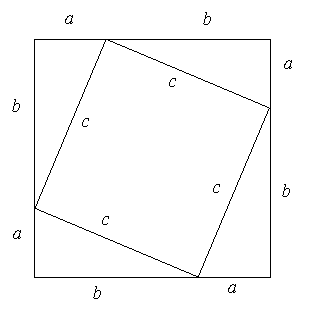 |
Figure4
4. Here
is a proof of the Pythagorean Theorem that uses a trapezoid rather than a
square. Complete the proof by writing the area of the trapezoid shown in
Figure5 in two different ways. Then equate your two formulas for the area of the
trapezoid and simplify to obtain ![]() Recall that the area A
of a trapezoid with parallel sides of lengths a and b and height h
is given by A =(1/2)(a + b)h.
Recall that the area A
of a trapezoid with parallel sides of lengths a and b and height h
is given by A =(1/2)(a + b)h.
 |
Figure 5
This proof of the Pythagorean Theorem is due to President James A. Garfield(1831-1881), who published it in the New England Journal of Education in 1876 (Dunham Problems, 8), before he was elected President of the United States in 1880. Garfield took office in January of 1881 and was assassinated later that year.
Instructor Notes
Objective: Students will verify the Pythagorean Theorem by computing areas of geometric figures, as mathematicians throughout history have done.
How to Use: Have students work on this activity individually or in small groups. Before students work on Problems 3 and 4, go over the example accompanying Figure 3 with them, making sure they understand the technique of writing the area of a figure in two different ways.
Solutions: 1a. 13 1b. 15 1c. 30
2a. Yes, by the converse of the Pythagorean Theorem
2b. No, by the Pythagorean Theorem
2c. No, by the Pythagorean Theorem
3. See Figure
4. Viewing the figure as a square with side length ![]() the area of the
figure is
the area of the
figure is ![]() . On the other hand,
dissecting the figure into four right triangles and one square, as shown,
yields area
. On the other hand,
dissecting the figure into four right triangles and one square, as shown,
yields area ![]() Equating these two
formulas for the area of the large square, we obtain
Equating these two
formulas for the area of the large square, we obtain
![]()
or ![]()
or ![]()
4. See
Figure5. Viewing the figure as a trapezoid with parallel sides of lengths a
and b and height ![]() the area of the figure
is
the area of the figure
is ![]() On
the other hand, dissecting the figure into three right triangles, as shown,
yields area
On
the other hand, dissecting the figure into three right triangles, as shown,
yields area ![]() Equating these two
formulas for the area of the trapezoid, we obtain
Equating these two
formulas for the area of the trapezoid, we obtain
![]()
or ![]()
or ![]()
or 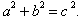
References: Activity from Lengths, Areas, and Volumes, by J. Beery, C. Dolezal, A. Sauk, and L. Shuey, in Historical Modules for the Teaching and Learning of Secondary Mathematics, Mathematical Association of America, Washington, D.C., 2003.
Dunham, William, Problems for Great Theorems (unpublished problem sets to accompany Journey Through Genius: The Great Theorems of Mathematics),Muhlenberg College, Allentown, Pennsylvania, 1994.
Swetz, Frank J., and T.I. Kao, Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China, National Council of Teachers of Mathematics, Reston, Virginia, 1977.