Archimedes' Estimate of π Activity

 

            The formula  for circle area is only as good as the approximation of π used in it. In Proposition 3 of his treatise, On the Measurement of the Circle, the Greek mathematician Archimedes (287-212 BCE) gave better estimates for π than were known previously.

 

Proposition 3. The ratio of the circumference of any circle to its diameter is less than 3 1/7 but greater than 3 10/71 (Dunham, 97; Katz, 109).

 

            What Archimedes is saying is that 3 10/71 < p < 3 1/7, or, rounding off to three places after the decimal point, 3.141 < p < 3.143. Archimedes' approximation of p was the first in history that was correct to two places after the decimal point!

 

 

 

 

 

 

 

 

 

 

 

 


                                                                                   

 

 

                                                                                   

 

 

 

 

 

 

 

 

 

 

 

 

 

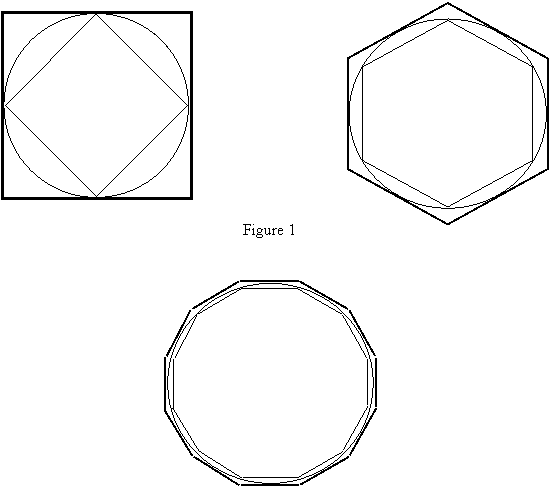
            Archimedes made the approximations 3 10/71 < p < 3 1/7 by estimating the circumference of a circle using the perimeters of inscribed and circumscribed polygons, such as those shown in Figure 1. If C is the circumference of the circle, r is its radius, and Pinsc and Pcirc are the perimeters of the inscribed and circumscribed polygons, respectively, then

 

Pinsc < C < Pcirc, or

 

Pinsc < 2pr < Pcirc, so that

 

Pinsc /2r < p < Pcirc /2r.

 

If we take the radius of the circle to be 1 (r = 1), then

 

Pinsc /2 < p < Pcirc /2.

 

            Archimedes started with inscribed and circumscribed regular hexagons. Since each of the six sides of a regular hexagon inscribed in a circle of radius 1 has length 1, then Pinsc = 6 in this case (see Problem 1a). Likewise, since each side of a regular hexagon circumscribed about a circle of radius 1 has length , then Pcirc =  (see Problem 1b). Hence, Pinsc /2 < π < Pcirc /2 yields , or .

 

            Archimedes then doubled the number of sides of each polygon to 12, obtaining an inscribed regular dodecagon of perimeter Pinsc =  (see Problem 1c), and a circumscribed regular dodecagon of perimeter Pcirc = 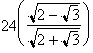. This yields 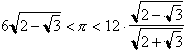, or 3.1058 < p < 3.2154. Archimedes proceeded to double the number of sides three more times until he had inscribed a regular 96-gon inside his circle and circumscribed another regular 96-gon about his circle, obtaining 3 10/71 < p < 3 1/7 (Dunham, 97-98; Johnson and Mowry, 404-405, 410).

 

            Archimedes' overestimate of p, p » 3 1/7 = 22/7, was used for hundreds of years afterwards by Greek mathematicians and by mathematicians of the next great mathematical civilization, the Arab Empire. Heron of Alexandria, a Greek mathematician who lived during the first century, wrote a very influential practical geometry book called the Metrica. Heron's formula for circle area in the Metrica was  which assumes p = 22/7 (Katz, 160, 162). This formula for circle area appeared in mathematical works for hundreds of years, including the work of one of the first great Arab mathematicians, Muhammad ibn Musa al-Khwarizmi, in the early ninth century (Katz, 268).

 

            Besides simply using Archimedes' estimate of p, later mathematicians also improved upon it by carrying out his technique with larger and larger numbers of inscribed and circumscribed polygons. In about 250 CE, the Chinese mathematician Liu Hui, who probably was not aware of Archimedes' work, used an inscribed polygon with 192 sides to obtain a slightly better approximation of p than Archimedes had made. Liu Hui or possibly a later Chinese mathematician then used a polygon with 3072 sides to obtain the estimate p » 3.1416. The Chinese mathematician Zu Chongzhi (or Tsu Ch'ung Chi, 429-500 CE) may have used a polygon with 24,576 sides (or possibly a more efficient method) to get 3.1415926 < p < 3.1415927 (Straffin, 173). French mathematician Francois Viete (1540-1603) used Archimedes' technique to estimate p correctly to 9 places. Viete began with a hexagon and doubled the number of sides of successive polygons 16 times to obtain a regular polygon with 393,216 sides (Dunham, 107). Just a few years later, in about 1600, Dutch mathematician Ludolph van Ceulen began with a square and doubled the number of sides of successive polygons 60 times to obtain a regular polygon with 262 sides and an estimate of p correct to 35 places (Dunham, 107-108).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

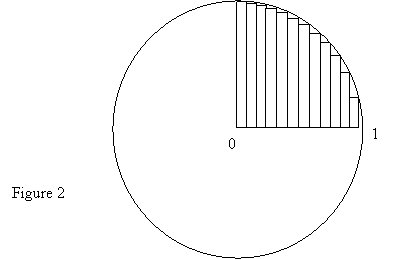
            Seventeenth century Japanese mathematicians may have estimated circle area, and hence p, using the method illustrated in Figure 2 (Beckmann, 125-127). Since the radius of the circle shown is 1, its area is p and the area of one quarter of the circle is p/4. By estimating the area of the quarter circle as the sum of the areas of the rectangular strips, one estimates p/4 and hence p. Using sums of areas of rectangles to estimate areas of regions having curved, rather than straight, boundaries is one of the fundamental ideas of integral calculus.

 

Beginning in the fifteenth century with the Indian mathematician Madhava, mathematicians have used infinite series (sum) formulas from calculus to obtain improved estimates of π. Today researchers are using computers to estimate p to billions of digits of accuracy.

 

In the following problems, you will use the method of Archimedes to estimate p.

 

1.         We use a regular hexagon inscribed in a circle of radius 1 to obtain the estimate

p » 3. See Figure 3. Since the hexagon is regular, it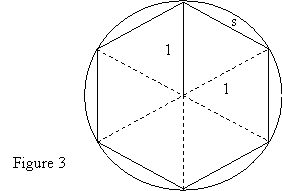s perimeter, Pinsc, is given by Pinsc = 6s, where s is the length of any one of its sides.

 

1a.       How large is each of the six angles at the center of the circle?    

 

1b.       How large are the other two angles (the base angles) in the isosceles triangle with sides labeled 1, 1, and s?

 

1c.       Find s and Pinsc.

 

1d.       Use the approximation C » Pinsc to estimate p.

 

2.         Now we use a regular hexagon circumscribed about a circle of radius 1 to obtain the estimate π » . See Figure 4a. Since the hexagon is regular, its perimeter, Pcirc, is given by Pcirc = 6s, where s is the length of any one of its sides. As you discovered in Problem 1, the six triangles formed by the sides of the hexagon are equilateral triangles. This time, however, each side has length s rather than 1. If we divide one of the equilateral triangles in half using a radius, as shown in Figure 4a, we obtain the right triangle with sides of lengths 1, (1/2)s, and s shown in Figure 4b.

 

2a.       Use the Pythagorean Theorem to find s.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


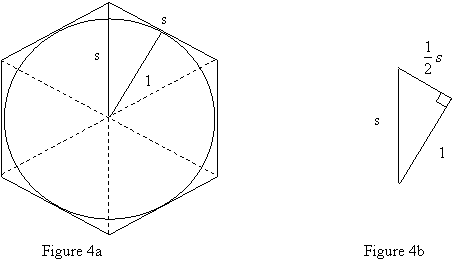
2b.       Compute Pcirc, then use the approximation C » Pcirc to estimate p.

 

 

3.         In this problem, we use a regular dodecagon inscribed in a circle of radius 1 to obtain the estimate π »  » 3.1058. See Figure 5a. Since the dodecagon is regular, its perimeter, Pinsc, is given by Pinsc = 12s, where s is the length of any one of its sides. We begin with the regular hexagon in Figure 3 and form a regular dodecagon by creating two new sides for each existing side, as shown in Figure 5a. Note that the new radius shown in Figure 5a bisects one side of the regular hexagon.

 

 

 

 

 

 

 

 

 

 

 

 

 


                                                                                   

 

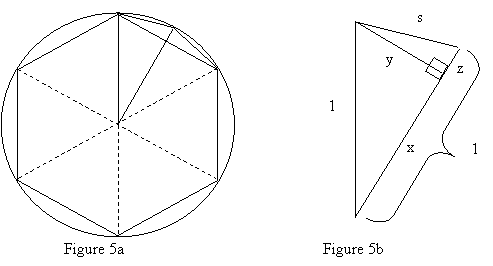
3a.       Refer to Figure 5b. Find y, then apply the Pythagorean Theorem to the right triangle with sides of lengths x, y, and 1 to find x.

 

3b.       Find z, then apply the Pythagorean Theorem to the right triangle with sides of lengths y, z, and s to find s.

 

3c.       Compute Pinsc, then use the approximation C » Pinsc to estimate p.

 

4.         In this problem, we obtain estimates of π using circumscribed and inscribed squares.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

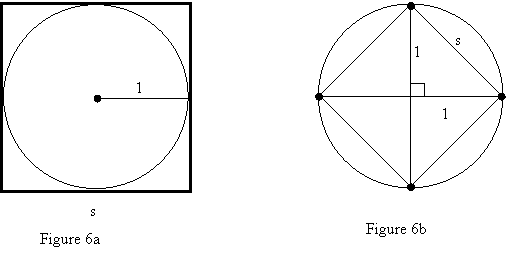
4a.       Find the side length s and perimeter, Pcirc, of a square circumscribed about a circle of radius 1, then use the approximation C » Pcirc to estimate p. See Figure 6a.

 

4b.       Find the side length s and perimeter, Pinsc, of a square inscribed in a circle of radius 1, then use the approximation C » Pinsc to estimate p. See Figure 6b.

 

4c.       Find the average of your two estimates from parts (a) and (b). Is the resulting estimate too large or too small?  

  

5.         In this problem, we use a regular octagon inscribed in a circle of radius 1 to obtain the estimate π »  » 3.0615. See Figure 7a. Since the octagon is regular, its perimeter, Pinsc, is given by Pinsc = 8s, where s is the length of any one of its sides. We begin with the square in Figure 6 and form a regular octagon by creating two new sides for each existing side, as shown in Figure 7a. Note that the new radius shown in Figure 7a bisects one side of the square.

 

 

 

 

 

 

 

 

 

 


                                                           

 

 

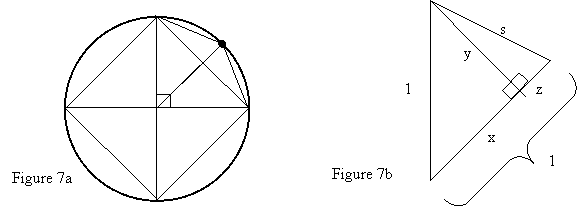
5a.       Refer to Figure 7b. Find x and y.

 

5b.       Find z, then apply the Pythagorean Theorem to the right triangle with sides of lengths y, z, and s to find s.

 

5c.       Compute Pinsc, then use the approximation C » Pinsc to estimate p.

 

6.         Show that the formula  for circle area is correct, if you replace

p by 22/7.

 

Instructor Notes

 

Objective: Students will investigate how Archimedes used perimeters of regular polygons to estimate p.

 

How to Use: Share with students, or have students read, information about the life and work of Archimedes. 

For Problems 1-7, students will need to use the theorem that the measures of the angles in any triangle sum to 180 degrees, along with the Pythagorean Theorem. You might remind them of the statements of these theorems, as well as of the definition of regular polygon. Note that Problems 1-3 form a complete set, as do Problems 4 and 5.

            Before or after completing Problems 3 and 5, you could have students show that if a regular n-gon inscribed in a circle of radius 1 has side length Sn, then the side length S2n of a regular 2n-gon inscribed in the same circle is given by

.

By repeated use of this formula, students may replicate Archimedes’ underestimate of p using the perimeter of an inscribed 96-gon, and may improve upon it by using inscribed polygons with even larger numbers of sides (Dunham Problems, 18; other sources for Problems 1-7: Harrigan, 1802-1804; Johnson and Mowry, 404-405, 410).

 

Related Activity: Hold a Pi Day celebration on March 14, preferably at 1:59 p.m.

 

Solutions:

 

1a.       360/6 = 60 degrees.

 

1b.       Since the triangle is isosceles, the two unknown angles are equal, let's say of measure

            . Since 60 + 2  = 180, then  = 60 degrees.

 

1c.       By part (b), the triangle is equilateral, so s = 1. Then Pinsc = 6s = 6.

 

1d.       C » Pinsc implies 2p » 6, which implies p » 3.

 

2a.       That s2 = 12 + ((1/2)s)2 implies s = .

 

2b.       Pcirc = 6s = .

            C » Pcirc implies 2p » , which implies p »  .

           

3a.       Since the radius labeled x + z = 1 bisects a line segment of length 1, y = 1/2.

Then x2 + y2 = 12 becomes x2 + (1/2)2 = 1, yielding x = .

3b.       Since , then s2 = y2 + z2 becomes ,

yielding s = .

 

3c.       Pinsc = 12s = , so that C » Pinsc implies 2p » ,

which implies p »   »  3.1058.        

 

4a.       We have s = 2, so that Pcirc = 4 x 2 = 8 and p » 4.

 

4b.       By the Pythagorean Theorem, s2 = 12 + 12, so that s = .

Then Pinsc =  and p »  » 2.8284.

 

4c.       Averaging the two estimates gives 2 +  » 3.4142, an overestimate of p.

 

5a.       Since the radius labeled x + z = 1 bisects a line segment of length , y = . Use the Pythagorean Theorem, or note that the triangle with sides of lengths x, y, and 1 is isosceles with legs of lengths x and y, to obtain x = .

 

5b.       Since , then s2 = y2 + z2 becomes ,

yielding s = .

 

5c.       Pinsc = 8s = , so that C » Pinsc becomes 2p » ,

which implies p »   or 3.0615.

 

6.         If we replace r by D/2 in the formula  we obtain  

If we replace p by 22/7 in the formula  we obtain

 

References: Activity from Lengths, Areas, and Volumes, by J. Beery, C. Dolezal, A. Sauk, and L. Shuey, in Historical Modules for the Teaching and Learning of Secondary Mathematics, Mathematical Association of America, Washington, D.C., 2003.

 

Beckmann, Petr, A History of Pi, St. Martin's Press, New York, 1971.

 

Dunham, William, Journey Through Genius: The Great Theorems of Mathematics, John Wiley and Sons, New York, 1990.

 

Dunham, William, Problems for Great Theorems (unpublished problem sets to accompany Journey Through Genius: The Great Theorems of Mathematics), Muhlenberg College, Allentown, Pennsylvania, 1994.

 

Harrigan, Mary, Activities for Mathematics 109, The Mathematical Experience (unpublished classroom activities), Nazareth College, Rochester, New York, 1995-1998.

 

Johnson, David, and Thomas Mowry, Mathematics: A Practical Odyssey, PWS Publishing, Boston, 1995.

 

Katz, Victor J., A History of Mathematics: An Introduction, Addison-Wesley, Reading, Massachusetts, 1998.

 

Straffin, Philip D., “Liu Hui and the First Golden Age of Chinese Mathematics,” Mathematics Magazine, 71 (1998), 163-181.

 

[back to Math 115 main page]

[back to main page]