Al-Khwarizmi’s Completing the Square Activity
The
general quadratic (degree 2) equation is of the form 
and can be solved
using the quadratic formula. Egyptian, Mesopotamian, Chinese, Indian, and Greek
mathematicians solved various types of quadratic equations, as did Arab
mathematicians of the ninth through the twelfth centuries. These Arab
mathematicians lived in an empire which extended from Spain and Morocco in the West to Pakistan in the East, and which was unified by a common scientific
language, Arabic, and a common religion, Islam.
One of the earliest of the Arab mathematicians, Muhammad ibn Musa al-Khwarizmi (approximately 780-850 CE), was employed as a scholar at the House of Wisdom in Baghdad in present day Iraq. Al-Khwarizmi wrote a book on the subjects of al-jabr and al-muqabala. Al-Khwarizmi's word al-jabr eventually became our word algebra, and, of course, the subject of his book was what we call algebra. Incidentally, the name al-Khwarizmi became our word algorithm (this one is a bit more of a stretch!). In his algebra book, al-Khwarizmi solves the following problem (Katz, 245):
What must be the square which, when increased by ten of its own roots, amounts to 39?
The equation al-Khwarizmi wanted to solve is 
. Today,
we probably would solve this equation by subtracting 39 from both sides, then
factoring. Al-Khwarizmi instead used the technique of completing the square. To
complete the square, we add (10/2)2 = 52 = 25 to both
sides of the equation, obtaining 
The lefthand side thus
becomes a perfect square (as does the right-hand side, in this example), and we
can write the equation as 
To solve the equation, we
take the square root of each side, obtaining 
or 
so that 
or 
Al-Khwarizmi
did not consider the negative solution; his solution was Since the original
problem asked for the square, he also noted that 
Al-Khwarizmi
had mastered Euclid’s Elements (c. 300 BCE)
and he, like Euclid, viewed what we would call algebra very
geometrically. As a result, when al-Khwarizmi solved the equation by
completing the square, he completed an actual square, as shown at right. The
solid line portion of the figure has area 
Just as the expression 
is not
yet a perfect square, the solid-line figure representing it also is not yet a
perfect square. To complete the square, we sketch in the dotted lines in the
lower righthand corner, adding a square region of area 52 = 25 to
the figure. Notice that the completed square has side length 
so has
area 
On
the other hand, if we compute the area piece by piece, the completed square has
area 
(That
was
given in the original problem.) Hence, Al-Khwarizmi then would
conclude that so that 
and
Al-Khwarizmi gave his instructions for solving the problem in words rather than symbols, as follows (Katz, 245):
What must be the square which, when increased by ten of its own roots, amounts to 39? The solution is this: You halve the number of roots, which in the present instance yields five. This you multiply by itself; the product is 25. Add this to 39; the sum is 64. Now take the root of this which is eight, and subtract from it half the number of the roots, which is five; the remainder is three. This is the root of the square which you sought for.
Al-Khwarizmi lived in Baghdad, in the heart of what had been ancient Mesopotamia, and the geometric techniques he used to solve various quadratic equations, together with the verbal instructions he gave for solving them, were quite similar to those of the much earlier Mesopotamian mathematicians (Katz, 246).
Later Arab mathematicians and Renaissance Italian mathematicians were interested in solving cubic equations; they succeeded in solving these equations by---you guessed it!---"completing the cube."
Problems from al-Khwarizmi’s al-Jabr:
1. Translate the following problem into a modern algebraic equation. Find both solutions of the equation using the method of completing the square, then draw the completed square representing the equation.
What must be the square which, when increased by eight of its own roots, amounts to 20?
2. In order to solve
the following problem, first draw a diagram with the length of the side of the
square denoted by x. Work out your own solution, then explain how
al-Khwarizmi obtained the equation 
.
Given an isosceles triangle with base 12 and legs each equal to 10, inscribe a square inside the triangle with one side along the base and the other two vertices on the legs. What is the side of the square?
Instructor Notes
Objective: Students will understand geometrically the technique of completing the square.
Solutions:
1. The equation to be solved is 
. To
complete the square algebraically, we add (8/2)2 = 42 =
16 to each side of the equation, obtaining 
= 
or 
Then 
and 
or 
Or,
students may argue geometrically as follows. The completed square shown at
right has side length 
so has area 
However,
if we compute the area piece by piece, the completed square has area 
= 
= 
(That was
given.) Hence, 
so that and or
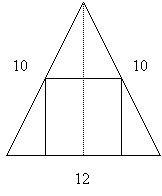2. Bisecting the isosceles triangle with the altitude
creates two right triangles, each with sides of lengths 6, 8, and 10 units. (Use
the Pythagorean Theorem or knowledge of 3-4-5 right triangles to see that the altitude is 8 units.)
Therefore, the area of the large triangle is 48 square units. Letting x
be the length of the side of the square, the square has area x2.
The two small triangles on either side of the square each have base length 
and
height x, so that their area together is 
. The triangle above the
square has base length x and height 
, so its area is 
. The sum
of the three areas is the total area, 48 square units, so that . This
equation can be simplified to 10x = 48, or x = 4.8 units.
References: Activity from Lengths, Areas, and Volumes, by J. Beery, C. Dolezal, A. Sauk, and L. Shuey, in Historical Modules for the Teaching and Learning of Secondary Mathematics, Mathematical Association of America, Washington, D.C., 2003.
Katz, Victor J., A History of Mathematics: An Introduction, Addison-Wesley, Reading, Massachusetts, 1998.