[Today’s class: Ancient Egyptian mathematics, continued, including
method of false position for solving linear equations (including example of two equations in two unknowns from ancient Mesopotamia), and
calculation of volume of frustum of pyramid (see Greatest Egyptian Pyramid activity on what constitutes a “formula”); and
Magic Squares activity]
Mathematics 115
Homework Assignment #7
Due Thursday, January 17, 2002
There is no getting out of it. Through and through the world is infected with quantity.
To talk sense is to talk in quantities. . . . You cannot evade quantity. You may fly
to poetry and to music, and quantity and number will face you in your rhythms
and your octaves. Elegant intellects which despise the theory of quantity
are but half developed. They are more to be pitied than blamed.
-Alfred North Whitehead in The Aims of Education, 1917
_______________________________________________________________________
Prof. Beery's office hours: Wednesday 1/16 11 a.m.-12:30 p.m., 4-5 p.m.
Thursday 1/17 11 a.m.-12:30 p.m., 4-5 p.m.
Friday 1/18 2:30 - 4:30 p.m.
and by appointment Hentschke 203D, x3118
Tutorial session: Day: ____________, Time: ____________, Place: ______________
_______________________________________________________________________
Read: "Mathematics in Early Civilizations" (pages 44-50: "Three Problems from the
Rhind Papyrus"---see especially pages 44 and 48)
Do: 1. What aspect of their mathematics does the author say prevented the ancient
Egyptians from progressing beyond "applied arithmetic"?
2. Problem 22 on page 50. You may solve the problem using modern algebraic
methods. Note that in order to express the answer in the Egyptian fashion,
you must find the answer as a fraction, not a decimal, then write it as a sum
of unit fractions.
3. Questions 1-5 from the Egyptian Method of Solving Equations handout.
Note that you are required to use false position in Questions 2 and 3 only.
You may give your answer to Question 5 in ro.
Read: "Learning the Ropes: The Origins of Geometry"
“Lengths, Areas, and Volumes” (end of the first section)
Do: 4. What does the author of “Learning the Ropes” claim is the "usual and
appropriate" definition of a straight line?
5. What is his explanation as to why Euclid defined straight line in the way
he did (instead of in the "usual and appropriate" way)?
Read: "Egyptian Geometry" (pages 384-390)
Do: 6. Exercises 1, 3, 5, 7, 18, and 20 from pages 395 and 396
Thursday's quiz (20 points) covers today’s class and Assignment #7 (above).
Lengths, Areas, and Volumes
Accurate measurement of length, area, and volume has been important throughout human history in agriculture and architecture. In ancient Egypt, both the farmer and the pyramid-builder needed to measure lengths, areas, and volumes, the farmer to determine the sizes of fields and crops and the pyramid-builder to determine the dimensions of the pyramid and its building blocks. Since the Industrial Revolution, accurate measurements have become increasingly important in manufacturing, science, and the development of technology. Today, physicists use a tiny unit called an angstrom (A), equal to one ten millionth of a millimeter, to measure electromagnetic wavelengths. Astronomers, on the other hand, use gigantic units to measure the distances between planets and stars. An astronomical unit (AU), equal to approximately 93 million miles or 150 million kilometers, is the mean distance of the earth from the sun, so is handy for measuring distances between planets in our solar system. A light-year, equal to approximately 5.88 trillion miles or 9.46 trillion kilometers, is the distance traveled by light in one mean solar year and is the unit used to measure distances between stars. All three of these units were invented in about 1900, in response to scientists' need and ability to measure very small and very large distances.
What units of measurement were needed in ancient Egypt, an agrarian society with an avid interest in pyramid-building? The basic unit for measuring length was the cubit, the distance from a person's elbow to the end of her middle finger. Smaller units included the palm and the finger. To measure the length of the side of a field or of a pyramid, an Egyptian might use a unit of measurement called a khet, equal to 100 cubits (Johnson and Mowry, 386). The finger and the khet were, respectively, the smallest and the largest units of length needed for most purposes in the agricultural society of the ancient Egyptians; these units, along with units for area and volume based upon them, were invented to meet the needs of that civilization.
Since farmers must measure lengths of irrigation channels, areas of fields, and volumes of harvested crops, many historians believe that practical geometry---formulas for measuring length, area, and volume---originated in the earliest agricultural civilizations on earth. The very earliest such civilization, called the Mesopotamian civilization, arose in the Fertile Crescent formed by the Tigris and Euphrates Rivers of what is now Iraq in about 3500 BCE.[1] Other early agrarian civilizations developed along the Nile River of Egypt, the Huang (Yellow) and Yangtze Rivers of China, the Indus River of what is now Pakistan, and the Ganges River of India, well before the Common era. Such civilizations are believed to have arisen slightly later in the Americas, probably due to the slower retreat of the glaciers in the Western Hemisphere after the last Ice Age and perhaps due to later human habitation of the Americas.[2] For example, while the Mayan civilization of Central America may be traced back to approximately 1500 BCE, it flourished from approximately 200 to 800 CE.
The Greek historian Herodotus (484-425 BCE) credits ancient Egyptian "rope-stretchers" with inventing geometry (Burton, 51; Dauben, 2). Due to the annual flooding of the Nile River, farmland had to be resurveyed each year so that it could be taxed fairly. Surviving wall paintings and documents indicate that the royal surveyors---or harpedonaptai, or rope-stretchers---measured the lengths of fields with ropes with equally spaced knots tied in them. Surveying was done by rope-stretchers in Mesopotamia and the Middle East, as well as in Egypt (Dauben, 2). In fact, the word geometry means earth (gea or geo) measurement (metria) in Greek and Latin (Burton, 51; Dauben, 2). Other geometric terms refer more directly to measurement using ropes; for instance, the word hypotenuse means "that which is stretched across" in Greek, connoting a rope stretched tightly between the two legs of a right triangle (Dauben, 3).
All of the early civilizations listed above had correct formulas for the areas of rectangles and triangles (Katz, 19). It seems likely that early peoples noticed that the area of a rectangle can be computed as the length of its base times its height by counting square units, as illustrated in Figure 1. They
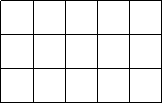 |
Figure 1.
|
probably obtained the area A of a right triangle as A = (1/2)bh by noticing that two copies of the right triangle make a rectangle of area bh, as in Figure 2.
 |
Figure 2.
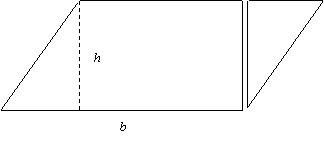
To see that the formula A = (1/2)bh gives the area of any triangle of base length b and altitude h, they might have noticed that two copies of the triangle form a parallelogram. The area of this parallelogram, after rearrangement, can be seen to be bh; hence, the area of the triangle is (1/2)bh. See Figure 3.
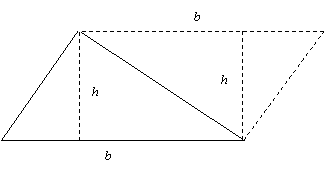 |
Figure 3.
 |
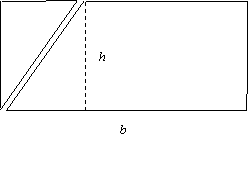 |
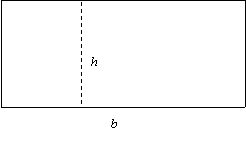 |
Note that Figure 3 also illustrates that the area of the parallelogram with base b and altitude h is bh.
The formula for the volume of a rectangular solid also was known in all of the early civilizations discussed above (Katz, 22). Early peoples probably noticed that in this case
Volume = length x width x height
by counting cubic units as illustrated in Figure 4.
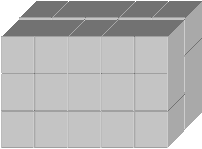
Figure 4.
|
References:
Burton, David, The History of Mathematics: An Introduction, McGraw-Hill, New York, 1997.
Dauben, Joseph W., “Learning the Ropes: The Origins of Geometry,” in Historical Notes: Mathematics Through the Ages, Consortium for Mathematics and Its Applications (COMAP), Lexington, Massachusetts, 1992.
Johnson, David, and Thomas Mowry, Mathematics: A Practical Odyssey, Brooks/Cole, Pacific Grove, California, 2001.
Katz, Victor J., A History of Mathematics: An Introduction, Addison-Wesley, Reading, Massachusetts, 1998.
Janet L. Beery
University of Redlands